
इस लेख में शामिल अन्य महत्वपूर्ण टॉपिक्स – mensuration formula in hindi pdf | mensuration all formula in hindi | mensuration 2d and 3d formula pdf in hindi | mensuration 2d and 3d formula pdf in hindi | mensuration 2d formula in hindi | all mensuration formula in hindi | mensuration 3d formula in hindi
लेकिन इन Mensuration formula in Hindi को जानने से पहले हम निम्नलिखित महत्वपूर्ण परिभाषाओं के बारे में जानेंगे, क्योंकि इन्हीं से संबधित यहाँ Mensuration formula in Hindi दिए गए हैं-
Mensuration in Hindi परिभाषा : Mensuration Definition के अनुसार क्षेत्रमिति यानि Mensuration गणित का वह भाग है जिसके अंतर्गत ज्यामितीय आकृतियों को मापने का अध्ययन किया जाता है। इसमें दो-आयामी (2-Dimensional shapes) और त्रि-आयामी (3-Dimensional) वस्तुओं के आकार, लंबाई, चौड़ाई, क्षेत्रफल और आयतन की गणना करने के लिए सूत्रों और सिद्धांतों का उपयोग किया जाता है।
दैनिक जीवन में क्षेत्रमिति का उपयोग वास्तुकला, इंजीनियरिंग और निर्माण सहित कई क्षेत्रों में किया जाता है।
क्षेत्रफल (Area) – हर एक वस्तु कुछ-ना-कुछ जगह घेरती है। किसी द्वि-आयामी यानि 2D (2 Dimensional) आकृति द्वारा घेरी गई जगह की मात्रा को ही उस आकृति का क्षेत्रफल कहते हैं। वह वस्तु कोई बंद आकृति भी हो सकती है। सभी आकृतियों का क्षेत्रफल उनके आकार पर निर्भर करता है। अलग-अलग आकृतियों के अलग-अलग क्षेत्रफल होते हैं।
क्षेत्रफल को हम इकाई वर्ग (square) में मापते हैं यानि कि क्षेत्रफल की मानक इकाई वर्ग इकाई है जिसे आम तौर पर वर्ग सेमी (Square cm), वर्ग फुट (square foot), वर्ग इंच (square inch), वर्ग मीटर (square meters) आदि के रूप में दर्शाया जाता है।
जैसे नीचे दिए चित्र में एक वर्ग है जिसके सभी भुजाओं की लंबाई 1 सेमी है। तो इसका क्षेत्रफल होगा – 1 वर्ग सेमी (1 cm 2 )

आयतन (Volume)– प्रत्येक त्रि-आयामी (3 Dimensional) वस्तु कुछ स्थान घेरती है। इस तरह उसके द्वारा घेरे गए स्थान की मात्रा को ही उसके आयतन के रूप में मापा जाता है। यदि वह वस्तु अंदर से खाली है तो उसमें व्याप्त स्थान उसके आयतन के रूप में परिभाषित किया जाता है। इसे वस्तु की क्षमता (capacity) के रूप में भी जाना जाता है।
इस तरह किसी वस्तु का आयतन ज्ञात करने से हमें ज्ञात होता है कि उसे भरने के लिए किसी पदार्थ की कितनी मात्रा की जरूरत है।
आयतन को हम इकाई घन (cube) में मापते हैं यानि कि आयतन की मानक इकाई घन इकाई है जिसे आम तौर पर घन सेमी (cm 3 ), घन फुट (foot 3 ), घन इंच (inch 3 ), घन मीटर (meter 3 ) आदि के रूप में दर्शाया जाता है।
2D और 3D वस्तु – 2D का full form होता है 2-Dimensional यानि द्वि-आयामी। ऐसे वस्तु जिनमें केवल दो आयाम हों उन्हें द्वि-आयामी वस्तु कहते हैं। इनमें केवल लंबाई और चौड़ाई ही होते हैं और अक्सर इन्हें हम x अक्ष (x axis) और y अक्ष (y axis) से इंगित करते हैं।
3D का full form होता है 3-Dimensional यानि त्रि-आयामी। ऐसे वस्तु जिनमें तीन आयाम हों उन्हें त्रि-आयामी वस्तु कहते हैं। इनमें लंबाई, चौड़ाई और ऊंचाई होते हैं और अक्सर इन्हें हम x अक्ष (x- axis), y अक्ष (y-axis) और z अक्ष (z-axis) से इंगित करते हैं।
परिमाप (Perimeter) – किसी समतल आकृति की सीमा की कुल लंबाई को उस आकृति का परिमाप कहा जाता है। यह परिमाप आकृति को घेरने वाली सभी भुजाओं या किनारों की लंबाई को जोड़कर निर्धारित किया जाता है। इसे सेंटीमीटर, मीटर, इंच या फीट जैसी माप की रैखिक इकाइयों में मापा जाता है।
ऊपर दी गई परिभाषाएं, जिनमें Mensuration Meaning in Hindi भी दी गई हैं, बहुत ही महत्वपूर्ण हैं और अक्सर परीक्षाओं में पूछी जाती हैं। इस लेख में इन्ही से संबंधित Mensuration All formula in Hindi दिए गए हैं।
यहाँ हम जो Mensuration formula in Hindi बताने जा रहे हैं उनमें परिमाप, क्षेत्रफल और आयतन से संबंधित फॉर्मूले हैं। हमनें यहाँ Mensuration formula chart भी दिया है जिससे आप आसानी से इन्हें याद कर सकते हैं और Mensuration formula in Hindi pdf दिया है जिसे डाउनलोड कर सकते हैं।
Mensuration Formula के बाद हमनें कुछ महत्वपूर्ण Mensuration problems या mensuration questions को हल किया है।
यह भी पढ़ें- त्रिकोणमिति से संबंधित महत्वपूर्ण सूत्र Top 100 GK Questions in Hindi
Table of Contents
Mensuration all formula in Hindi : यहाँ पहले हमनें 2D आकृतियों के लिए Mensuration formula in Hindi दिया है और उसके बाद 3D आकृतियों के लिए Mensuration formula in Hindi दिया है। इससे आपको इन्हें याद करने में आसानी होगी।

परिभाषा : वर्ग एक ऐसी द्वि-आयामी आकृति है जिसमें 4 भुजाएँ और 4 शीर्ष होते हैं। वर्ग की सभी भुजायें आपस में बराबर होती हैं और सभी आंतरिक कोण समकोण होते हैं। जैसा कि नीचे चित्र में दिया गया है। यदि वर्ग की भुजा की लंबाई a हो तो –
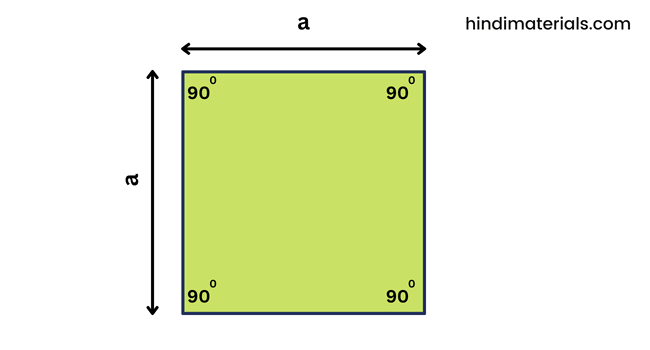
वर्ग का परिमाप (perimeter of square)= 4 × भुजा = 4 × a वर्ग का क्षेत्रफल (area of square) = (भुजा × भुजा) = भुजा2 = a² वर्ग का क्षेत्रफल = ½ × (विकर्णो का गुणनफल) = ½ × d2 वर्ग का विकर्ण (diagonal of square )= एक भुजा × √2 = a × √2 वर्ग का विकर्ण = √2 × वर्ग का क्षेत्रफल या d = √2 a²
परिभाषा : एक ऐसा चतुर्भुज (चार भुजाओं वाली आकृति) जिसकी सम्मुख भुजायें बराबर और समानांतर होती है और आंतरिक कोण समकोण होते हैं, उसे आयात कहा जाता है। आयात की आसन्न भुजायें बराबर नहीं होती हैं।
माना कि किसी आयात की लंबाई a और चौड़ाई b है तो –

आयत का परिमाप (perimeter of rectangle formula ) = 2(लम्बाई + चौड़ाई) = 2(a +b) आयत का क्षेत्रफल (area of rectangle )= लंबाई ×चौड़ाई = 2ab आयत का विकर्ण (diagonal of rectangle)=√(लंबाई² + चौड़ाई²) = √(a² + b²)
समचतुर्भुज एक ऐसा चतुर्भुज है जिसकी सभी भुजायें समान होती हैं और विपरीत भुजायें समांतर होती हैं। इसके आंतरिक कोण समकोण नहीं होते हैं और सम्मुख कोण समान होते हैं।
समचतुर्भुज और वर्ग में यह अंतर यह है कि समचतुर्भुज का कोई भी आंतरिक कोण समकोण नहीं होता है जबकि एक वर्ग के सभी कोण समकोण होते हैं।
जैसा कि नीचे चित्र में दिखाया गया है कि एक वर्ग और समचतुर्भुज में क्या अंतर है।
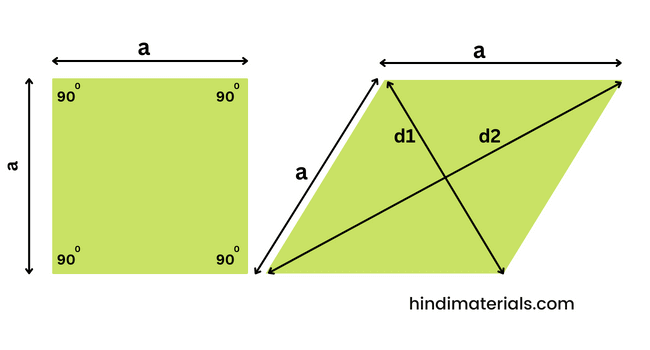
समचतुर्भुज से संबंधित सूत्र –माना किसी समचतुर्भुज की भुजा a, विकर्ण d1, d2 हैं और ऊंचाई h है, तो-
समचतुर्भुज का क्षेत्रफल = ½ × d1 x d2 या आधार x ऊंचाई = b x h समचतुर्भुज की परिमाप = 4 × भुजा = 4a • 4a² = (d1)² + (d2)²
एक समांतर चतुर्भुज एक विशेष प्रकार का चतुर्भुज होता है जिसमें विपरीत भुजायें एक दूसरे के समानांतर होती और लंबाई में बराबर होती हैं। साथ ही इसके विपरीत कोण माप में समान होते हैं।
समांतर चतुर्भुज और आयत में यह अंतर यह है कि समांतर चतुर्भुज का कोई भी आंतरिक कोण समकोण नहीं होता है जबकि एक आयत के सभी कोण समकोण होते हैं।
माना किसी समांतर चतुर्भुज की एक भुजा a, दूसरी भुजा b और ऊंचाई h है, तो –
क्षेत्रफल = आधार x ऊंचाई = a x h परिमाप = 2(लंबाई + चौड़ाई) = 2(a+b)
समलंब चतुर्भुज वह चतुर्भुज है जिसमें दो सम्मुख भुजायें आपस में समांतर होती हैं। यह जरूरी नहीं है कि इनकी लंबाई भी समान हो।
समलंब चतुर्भुज की समांतर भुजाओं को “आधार” (Base) कहा जाता है और अन्य दो भुजाओं को समलंब चतुर्भुज का “Leg” कहा जाता है।
समलंब चतुर्भुज के प्रकार
इस तरह के समलंब चतुर्भुज में असमांतर भुजाओं की लंबाई समान होती है। नीचे दिए गए Isosceles Trapezium में AD = BC

इस तरह के समलंब चतुर्भुज में सभी भुजायें और अन्तः कोण आसमान होते हैं।
इस तरह के समलंब चतुर्भुज में कम-से-कम दो आसन्न कोण समकोण होते हैं। नीचे दिए गए चित्र में कोण A = कोण D = 90 0

समलंब चतुर्भुज से संबंधित सूत्र
समलंब चतुर्भुज का क्षेत्रफल = ½ x (समांतर भुजाओं का योग) (समांतर भुजाओं के बीच की दूरी) = ½ x (a+b) h समलंब चतुर्भुज का Median या Mid-segment - समलंब चतुर्भुज में median एक ऐसी रेखा खंड जो दोनों असमांतर रेखाओं के मध्य बिंदुओं को जोड़ती है। नीचे दिए गए चित्र के अनुसार Median EF = (AB + DC) / 2

चक्रीय चतुर्भुज ऐसे चतुर्भुज को कहते हैं जिसके चारों शीर्ष किसी वृत्त की परिधि पर स्थित हों। नीचे दिए गए चित्र में ABCD एक चक्रीय चतुर्भुज है जिसके चारों शीर्ष वृत की परिधि पर स्थित हैं।
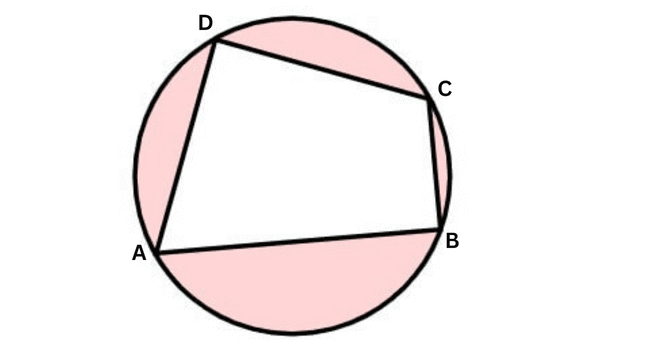
चक्रीय चतुर्भुज से संबंधित सूत्र –
∠A + ∠C = 180° ∠B + ∠D = 180° यदि किसी चक्रीय चतुर्भुज की भुजायें क्रमशः a, b, c और d हों तो चक्रीय चतुर्भुज की अर्धपरिधि s = (a+b+c+d)/2 चक्रीय चतुर्भुज का क्षेत्रफल = √(s−a)(s−b)(s−c)(s−d) परिवृत्त की त्रिज्या = 1/4A√(ab+cd)(ac+bd)(ad+bd) चक्रीय चतुर्भुज के विकर्ण = माना दिए गए चक्रीय चतुर्भुज के विकर्ण p और q हैं तो p = √(ac+bd)(ad+bc)/ab+cd और q = √(ac+bd)(ab+cd)/ab+bc
ऐसा त्रिभुज जिसकी सभी भुजायें बराबर हों। माना कि सभी भुजाओं की लंबाई a है तो –
समबाहु त्रिभुज का क्षेत्रफल = (√3)/4 × भुजा2 = (√3)/4 × a2 समबाहु त्रिभुज का शीर्षलम्ब = (√3)/4 × भुजा = (√3)/4 × a परिमाप = 3 × भुजा = 3 × a
ऐसा त्रिभुज जिसकी केवल दो भुजायें समान हों। माना कि समान भुजाओं की लंबाई a और तीसरी भुजा की लंबाई b हो तो
समद्विबाहु त्रिभुज का क्षेत्रफल = 1 / 4 b √ (4b² – a²) समद्विबाहु त्रिभुज का शीर्षलम्ब = a / 4 b √ (4b² – a²) परिमाप = 2a + b
ऐसा त्रिभुज जिसकी तीनों भुजायें आसमान हों। माना कि भुजाओं की लंबाई a, b और c है, तो –
परिधि = a + b + c और अर्धपरिधि s = ½ ( a + b + c )
विषमबहु त्रिभुज का क्षेत्रफल = √ s(s – a)(s – b)(s – c) इसे हीरों का फार्मूला (Heron's formula) भी कहते हैं।
दुसरें रूप में, A = ½ × आधार × ऊँचाई
अर्धपरिधि P = ½ ( a + b + c )
समकोण त्रिभुज का क्षेत्रफल, A = ½ × आधार × ऊँचाई
समकोण समद्विबाहु त्रिभुज का परिमाप = (2 + √2) × भुजा
समकोण समद्विबाहु त्रिभुज का कर्ण = (√2) × भुजा
समकोण समद्विबाहु त्रिभुज का क्षेत्रफल = ½ × भुजा 2
जैसा कि नाम से ही स्पष्ट है कि एक बहुभुज में कई भुजायें होती हैं। अर्थात बहुभुज एक ऐसा बंद दविमीय आकृति है जो कई रेखाखण्डों से मिलकर बना होता है। स्पष्ट है कि एक बहुभुज बनाने के लिए कम-से-कम तीन भुजाओं का होना जरूरी है। ये रेखाखण्ड जहां एक दूसरे से मिलती हैं उन्हें शीर्ष कहा जाता है।
भुजाओं की संख्या किसी बहुभुज के आकार को निर्धारित करती है और उस बहुभुज का नाम उसकी भुजाओं की संख्या के आधार पर रखा जाता है। जैसे 3 भुजा वाला बहुभुज -Triangle, 4 भुजा वाला बहुभुज- Quadrilateral, 5 भुजा वाला बहुभुज – Pentagon, 6 भुजा वाला बहुभुज – Hexagon, 7 भुजा वाला बहुभुज – Heptagon, 8 भुजा वाला बहुभुज – Octagon, 9 भुजा वाला बहुभुज – Nonagon, 10 भुजा वाला बहुभुज – Decagon. नीचे चित्र में एक Hexagon या षट्भुज दिया गया है-

बहुभुज से संबंधित महत्वपूर्ण सूत्र – माना कि एक n भुजा वाला बहुभुज है जिसकी सभी भुजायें एकसमान हैं तो-
n भुजा वाले बहुभुज के सभी अन्तः कोणों का योग = (n -2)1800 n भुजा वाले बहुभुज का प्रत्येक अंतः कोण = [(n-2)180°]/n n भुजा वाले बहुभुज के बहिष्कोणों का योग = 360° n भुजा वाले बहुभुज का प्रत्येक बहिष्कोण = 360°/n n भुजा वाले बहुभुज के विकर्णों की संख्या = [n(n-3)]/2 n भुजा वाले बहुभुज की परिमिति = n × a (जहां a एक भुजा की लंबाई है) n भुजा वाले बहुभुज का क्षेत्रफल = a/2tan(180/n) नियमित षट्भुज का क्षेत्रफल = (3a2 √3)/2
यदि दिए गए वृत्त की त्रिज्या r है तो –
वृत्त का व्यास (cord of a circle ) = 2r वृत्त की परिधि (circumference of a circle)= 2πr (जहां π = 22/7 या 3.142 (लगभग) वृत्त का क्षेत्रफल (Area of a circle)= πr² वृत्त की त्रिज्या = √व्रत का क्षेत्रफल/π
अर्द्धवृत्त की परिधि = ( π r + 2 r )
अर्द्धवृत्त का क्षेत्रफल = ½ (πr²)
एक वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो, उस वृत्त का एक त्रिज्यखंड कहलाता है। नीचे दिए गए चित्र में भाग APBO और OAQB, O केंद्र वाले वृत्त के दो त्रिज्यखंड हैं।
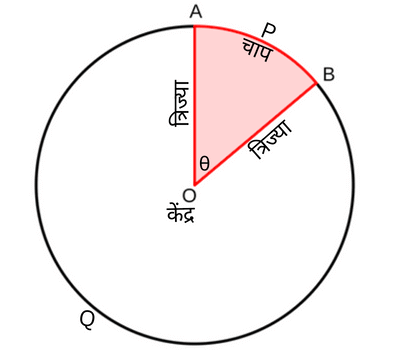
भाग APBO को लघु त्रिज्यखंड और भाग OAQB को दीर्घ त्रिज्यखंड कहते हैं।
माना कि त्रिज्यखंड APBO का कोण AOB का मान θ है तो
त्रिज्यखंड का क्षेत्रफल A = (θ/360°) × πr2 यदि कोण रेडियन में है तो त्रिज्यखंड का क्षेत्रफल A = (θ/2) × r2 त्रिज्यखंड के संगत चाप APB की लंबाई = (θ/360) × 2πr या (θπr) /180 यदि त्रिज्यखंड का कोण ज्ञात ना हो तथा चाप और त्रिज्या की लंबाई ज्ञात हो तो त्रिज्यखंड का क्षेत्रफल - (l × r)/2 (जहाँ l चाप की लंबाई और r त्रिज्या है) त्रिज्यखंड की परिमिति - 2r+ ((θ/360) × 2πr )
वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो एक वृत्तखंड कहलाता है। ऊपर दिए गए चित्र में AB केंद्र O वाले वृत्त की एक जीवा है। इसमें छायांकित भाग APB एक लघु वृत्तखंड है और अछायांकित भाग AQB दीर्घ वृत्तखंड है।

वृत्तखण्ड APB का क्षेत्रफल = r2 [πθ/360° - sinθ/2] (जब θ डिग्री में है ) या (r2 / 2) [θ - sin θ] (जब θ रेडियन में है) वृत्तखण्ड APB की परिमिति = rθ + 2r sin (θ/2), यदि 'θ' डिग्री में है या πrθ/180 + 2r.sin(θ/2), यदि 'θ' रेडियन में है।
यह एक त्रिआयामी (3 Dimensional) आकृति है जिसमें कुल 6 वर्गाकार फलक या पृष्ठ होते हैं। घन में कुल 12 कोर (भुजायें) और 8 शीर्ष होते हैं। माना कि किसी घन की भुजा a है तो-
घन का आयतन = a3 पार्श्वपृष्ठ का क्षेत्रफल - 4 a² घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a² घन का विकर्ण d = a√3 पृष्ठ का विकर्ण = a√2 घन का परिमाप = 12a घन के अंदर स्थित सबसे बड़े गोले (inscribed sphere) की त्रिज्या = a/√2 एक घन के बाह्य गोले की त्रिज्या, जो घन को घेरने वाले सबसे छोटे संभव गोले की त्रिज्या = a x √3/2
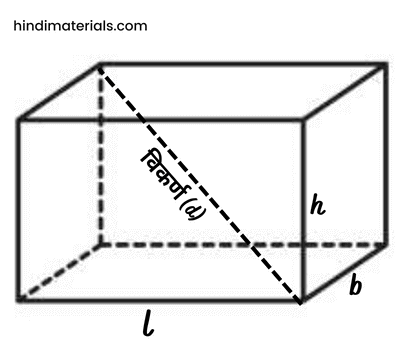
घन की तरह इसमें भी 6 फलक या पृष्ठ, 12 कोर (भुजायें) और 8 शीर्ष होते हैं। लेकिन ये फलक आयताकार होते हैं। इसलिए घनाभ की ऊंचाई, लंबाई और चौड़ाई एकसमान नहीं होते हैं। माना किसी घनाभ की लंबाई l, चौड़ाई b और ऊंचाई h है तो-
घनाभ का आयतन = लंबाई x चौड़ाई x ऊंचाई = l × b × h घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2 [( l × b ) + ( b× h ) + ( l× h )] घनाभ के सबसे लंबे विकर्ण की लंबाई d = √(l² + b² + h²) घनाभ का परिमाप - 4(l + b+l) घनाभ के पार्श्व सतह का क्षेत्रफल = 2h ( l + b )

माना कि किसी बेलन की त्रिज्या r और ऊंचाई h है तो –
बेलन का आयतन = πr2h बेलन के वक्रपृष्ठ का क्षेत्रफल = 2πrh बेलन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2πr ( h + r ) बेलन की त्रिज्या = √(आयतन / πh) बेलन के आधार का क्षेत्रफल = πr2
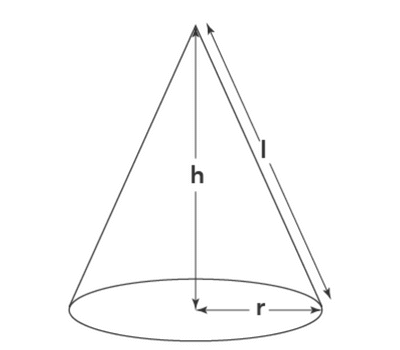
शंकु के शीर्ष से वृत्ताकार आधार के केंद्र तक की दूरी को शंकु की ऊंचाई h कहते हैं और शीर्ष से आधार की परिधि पर स्थित किसी बिन्दु की दूरी को शंकु की तिरछी या तिर्यक ऊंचाई l कहते हैं। माना कि वृत्ताकार आधार त्रिज्या r है तो-
शंकु की तिर्यक ऊँचाई l = √(h2 + r2) शंकु के आधार का क्षेत्रफल- πr2 शंकु के वक्र पृष्ठ का क्षेत्रफल = πrl शंकु के कुल पृष्ठ का क्षेत्रफल = πr2 + πrl = πr(r + l) शंकु का आयतन = 1/3 πr2h शंकु की ऊँचाई h = √(l2 – r2 ) शंकु की आधार की त्रिज्या = √(l2 – h2 )
Frustum क्या है – जब शंकु के असमतल भाग की तरफ का कुछ भाग समतल भाग के समांतर काट दिया जाता है तो शेष बचे ठोस को शंकु का छिन्नक कहते हैं। यह उल्टे गिलास या उल्टी बाल्टी की तरह दिखाई देता है। इस तरह एक छिन्नक की दो त्रिज्याएं बन जाती हैं – एक बड़े वृत्तीय समतल की त्रिज्या OC (माना R) और एक छोटे वृत्तीय समतल की त्रिज्या QA (माना r)।

माना छिन्नक की तिरछी ऊंचाई l और ऊंचाई h है तो
शंकु के छिन्नक की तिरछी ऊंचाई l = √[h2 +(R-r)2] शंकु के छिन्नक का आयतन = ⅓ π(R² + r² + Rr)h या ⅓ πh[ (R3 - r3) / r ] शंकु के छिन्नक के वक्र पृष्ठ का क्षेत्रफल = π(R + r)l शंकु के छिन्नक के कुल पृष्ठ का क्षेत्रफल = π[l(R+r) +R2 +r2]
परिभाषा : प्रिज्म एक बहुफलक (polyhedron) त्रि-आयामी आकार है जिसमें एक दूसरे के समांतर दो बहुभुज आधार (polygonal bases) होते हैं। ये दो बहुभुज आधार पार्श्व फलकों द्वारा जुड़े हुए हैं। पार्श्व फलक आयत या समांतर चतुर्भुज हो सकते हैं। A prism is a polyhedron three-dimensional shape consisting of two polygonal bases parallel to each other. These two polygonal bases are joined by lateral faces. The lateral faces may be rectangle or parallelogram.

प्रिज्म विभिन्न प्रकार के होते हैं, जिनका नाम उनके आधार के आकार के अनुसार रखा जाता है और उनसे संबंधित फॉर्मूले भी भिन्न-भिन्न होते हैं। लेकिन निम्नलिखित दो फॉर्मूले साधारणतया प्रयोग किए जाते हैं-
प्रिज्म का कुल सतह क्षेत्रफल (Total Surface area of a prism) = 2 × आधार का क्षेत्रफल + पार्श्व सतहों का क्षेत्रफल प्रिज्म का आयतन (Volume ) = आधार का क्षेत्रफल × ऊंचाई
प्रिज्म के प्रकार और उनसे संबंधित फॉर्मूले-
प्रिज्म विभिन्न प्रकार के होते हैं। इनका नाम प्रिज्म के आधार के आकार के के अनुसार रखा गया है। जैसे- Rectangular Prism, Triangular Prism, Pentagonal Prism और Hexagonal Prism.
Rectangular Prism – इस प्रकार के प्रिज्म में दोनों समानांतर आधार आयताकार होते हैं और 4 आयताकार पार्श्व पृष्ठ होते हैं। Rectangular Prism formula-
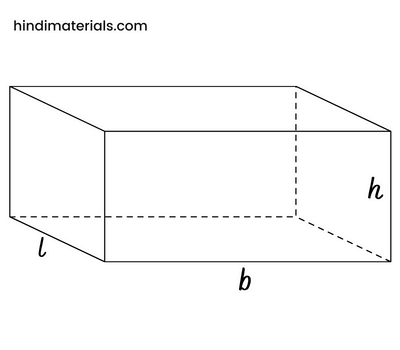
Rectangular Prism के आधार का क्षेत्रफल = b x l Rectangular Prism का पृष्ठीय क्षेत्रफल = 2(bl + lh + hb) Rectangular Prism का आयतन = l x b x h
Triangular Prism – इस प्रकार के प्रिज्म में दोनों समानांतर आधार त्रिभुजाकार (triangular) होते हैं और 3 आयताकार पार्श्व पृष्ठ होते हैं। Triangular Prism formula-

Triangular Prism के आधार का क्षेत्रफल = (1/2) × ab Triangular Prism का कुल पृष्ठीय क्षेत्रफल = ab + 3bh Triangular Prism का आयतन = (1/2) × abh
Pentagonal Prism – इस प्रकार के प्रिज्म में दोनों समानांतर आधार पंचभुजाकार (pentagonal) होते हैं और 5 आयताकार पार्श्व पृष्ठ होते हैं। Pentagonal Prism formula-
Pentagonal prism के आधार का क्षेत्रफल = (5/2) × ab Pentagonal prism का कुल पृष्ठीय क्षेत्रफल = 5ab + 5bh Pentagonal prism का आयतन = (5/2) × abh
Hexagonal Prism – इस प्रकार के प्रिज्म में दोनों समानांतर आधार षट्भुजाकार (hexagonal) होते हैं और 6 आयताकार पार्श्व पृष्ठ होते हैं। Hexagonal Prism formula-
Hexagonal prism के आधार का क्षेत्रफल = 3ab Hexagonal prism का कुल पृष्ठीय क्षेत्रफल = 6ab + 6bh Hexagonal prism का आयतन = 3abh
माना कि किसी गोले की त्रिज्या r है तो –
गोले का आयतन = (4/3) πr3 गोले के वक्रपृष्ठ का क्षेत्रफल = 4πr2
अंदर से खोखले गोले को गोलीय शेल कहा जाता है। इस तरह इसकी दो त्रिज्याएं होंगी- एक आंतरिक त्रिज्या (माना r) और एक बाह्य त्रिज्या (माना R)। तो –
गोलीय शेल का आयतन = (4/3)π ( R3 – r3 ) गोलीय शेल के आंतरिक पृष्ठ का क्षेत्रफल = 4π r2 गोलीय शेल के सम्पूर्ण पृष्ठ का क्षेत्रफल = 4π ( R2 + r2 )
जैसा कि नाम से ही स्पष्ट है, एक अर्द्ध गोला किसी गोले का आधा हिस्सा होता है। माना इस अर्द्ध गोले की त्रिज्या r है तो-
अर्द्ध गोले का आयतन = 2/3 πr3 अर्द्ध गोले के वक्रपृष्ठ का क्षेत्रफल = 2πr2 किसी अर्द्ध गोले के सम्पूर्ण पृष्ठ का क्षेत्रफल = 3πr2
Important Tags – mensuration formula in hindi pdf | mensuration all formula in hindi | mensuration 2d and 3d formula pdf in hindi | mensuration 2d and 3d formula pdf in hindi | mensuration 2d formula in hindi | all mensuration formula in hindi | mensuration 3d formula in hindi